
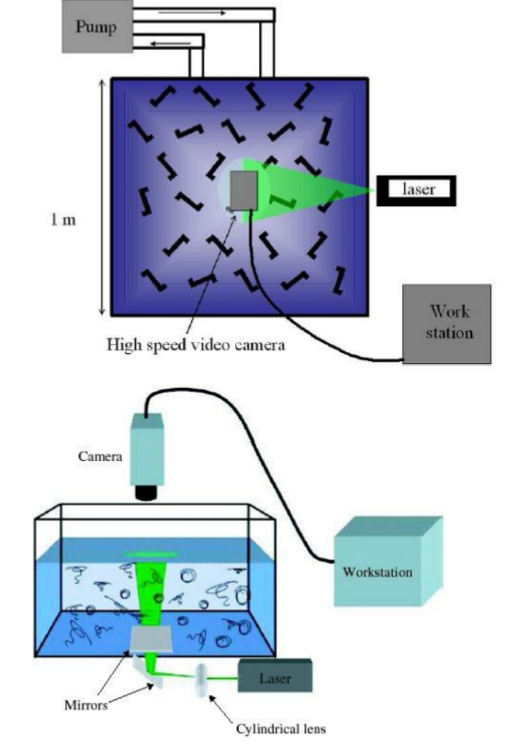
Building on the experiments performed for the project:
Time-Evolution of a Fractal Distribution:
Particle Concentrations in Free-Surface Turbulence
and
Power-law distributions of particle concentration in free-surface flows,
we studied the effect of spatial and temporal correlation of the flow field on the
resulting particle concentration field.
Turbulence is especially difficult to understand because
the velocity fluctuations, which lie at its heart, are chaotic in
both space and time. In an effort to capture the essence of turbulence,
Kraichnan
proposed that the turbulent velocity fluctuations are more easily understood by assuming that the
temporal fluctuations are delta correlated, as in
Brownian motion.
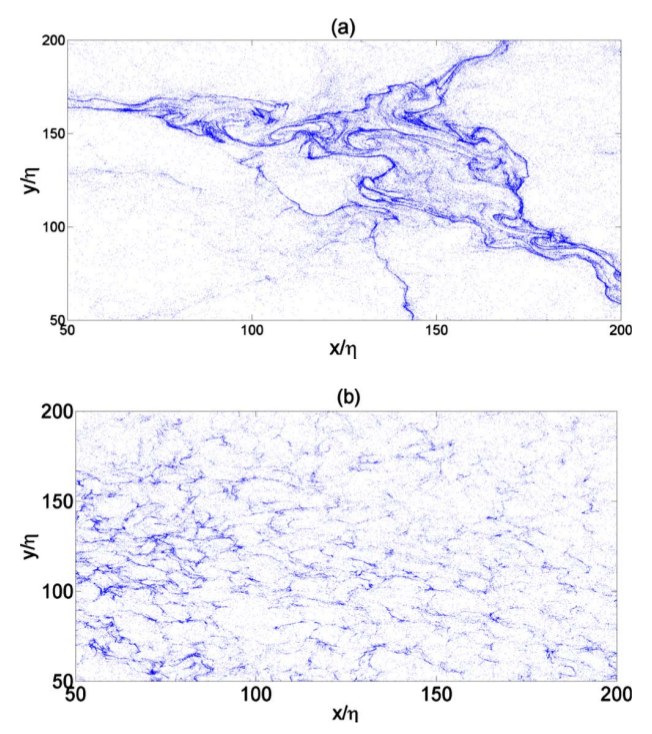
In Figure (a, correlated) above, the trajectories of the floating particles are generated using the velocity fields in the order they were taken experimentally. In Figure (b, decorrelated), the velocity sequence is randomly shuffled in time to generate new trajectories. This analysis
mimics the
Kraichnan ensemble and yields properties of a velocity
correlation function that is
delta correlated
in time but not in space.
Certain aspects of the particle motion and topology
are retained in the temporally decorrelated field.
The topology of the decorrelated floaters is string-like, just
as in the correlated case.
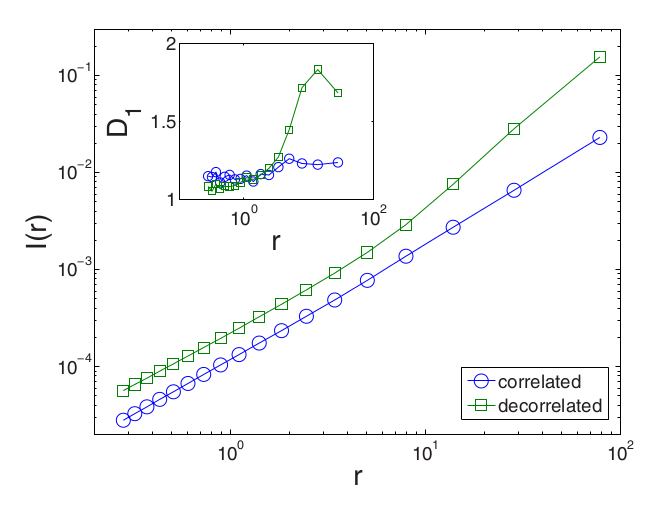
The
fractal information dimension D1 remains close to unity, at least
at small spatial scales where this parameter is defined. On
large scales, temporal decorrelation truncates the length of
the string-like structures, as seen in the above Figure (b).
The present measurements show that D1 is measurably altered by
the temporal randomization, but at small scales the particle
distribution retains its string-like character.
The measurements reported here demonstrate that our understanding of
turbulence can be enhanced by comparing and contrasting correlated
and temporally decorrelated flows.







