Jason Larkin's MS Projects
Time-Evolution of a Fractal Distribution: Particle Concentrations in Free-Surface Turbulence

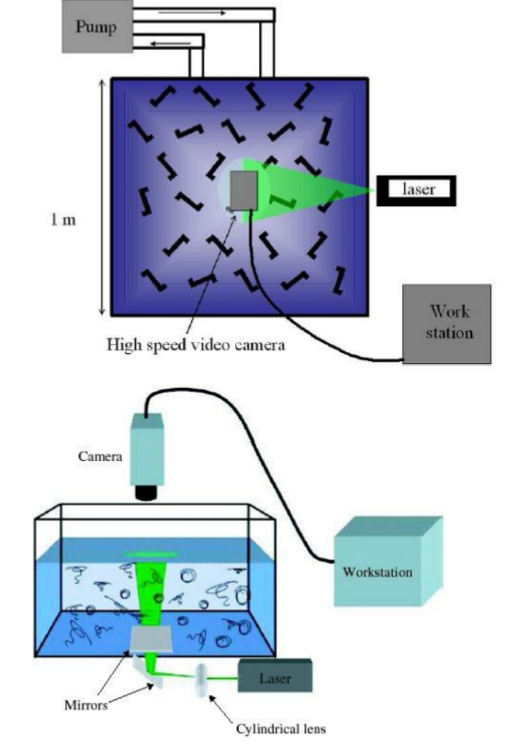
If the spatial particle distribution is initially uniform at t = 0, continuous motion of the underlying fluid evolves this spatial distribution into string-like structures. Ultimately a steady state is reached, at which time the floaters occupy a fractal dimension much less than 2. This time evolution into a fractal is a generic effect. It occurs even if the interactions between the floaters is negligibly small. A common manifestation of this phenomenon is the coagulation of scum on the surface of the sea, as is often seen in an ocean harbor.
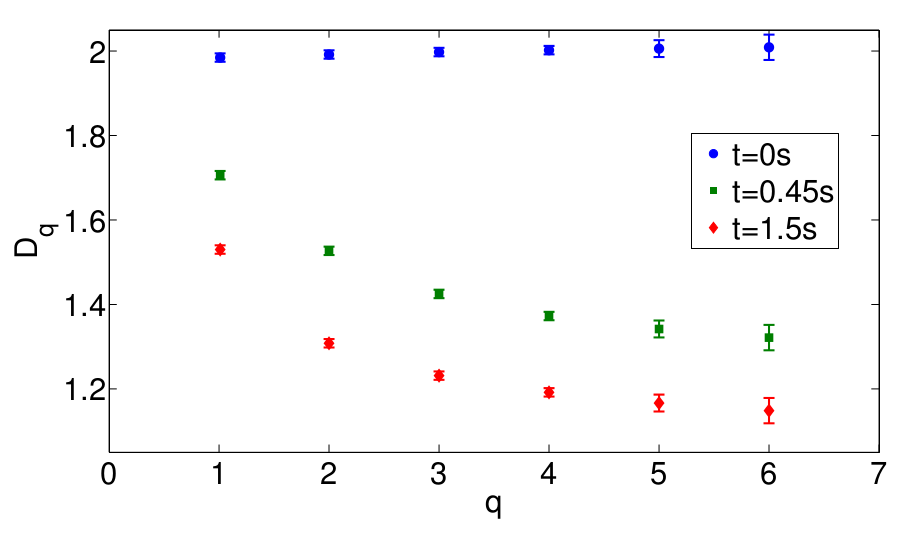
A range of values of the fractal dimensions Dq are measured for various times in the experiment. These results indicate a multi-fractal distribution of the particles for the inertial range of the flow after the particles evolve from a homogeneous one at t = 0 s. The system evolves in a time of the order of the lifetime of the largest eddies of the turbulent flow to a steady state where the measured Dq(t) approach a value that is slightly greater than 1, implying the formation of the string-like structures. The correlation dimension D2(t) evolves exponentially as the steady state is approached.
It is not possible, so far, to deduce these observations from the Navier-Stokes equations for the compressible flow studied here. A compressible system of particles in free-surface turbulence represents an instance of a chaotic attractor in real space. The analysis performed in this work uses the tools developed for chaotic and dynamical systems to study this complex coagulation phenomenon.