QGML Visualization Gallery

This page showcases the visualizations and analysis results generated by the QGML framework.

Advanced Quantum Geometry Analysis

The following visualizations were generated by running the geometric analysis demo, which demonstrates the advanced quantum geometry features of QGML including topological analysis, quantum information measures, and comprehensive geometric analysis.

Comprehensive Analysis Visualization

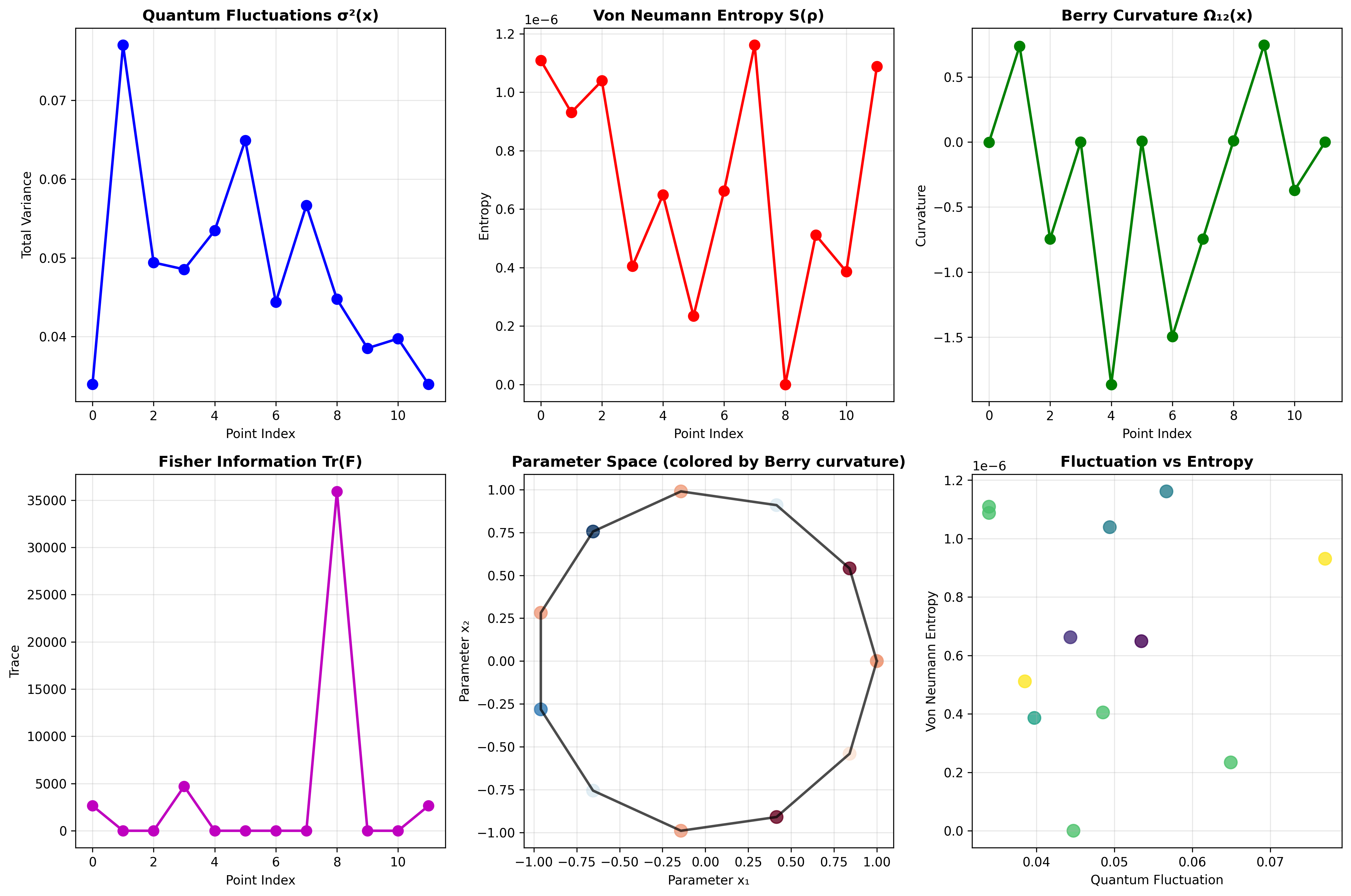
This comprehensive visualization shows six key aspects of quantum geometric analysis:

1. Quantum Fluctuations σ²(x): Total variance in quantum states across parameter space

2. Von Neumann Entropy S(ρ): Quantum information content of the density matrix

3. Berry Curvature Ω₁₂(x): Topological curvature in parameter space

4. Fisher Information Tr(F): Quantum Fisher information matrix trace

5. Parameter Space Trajectory: 2D parameter space colored by Berry curvature

6. Correlation Analysis: Relationship between quantum fluctuations and entropy

Topological Analysis

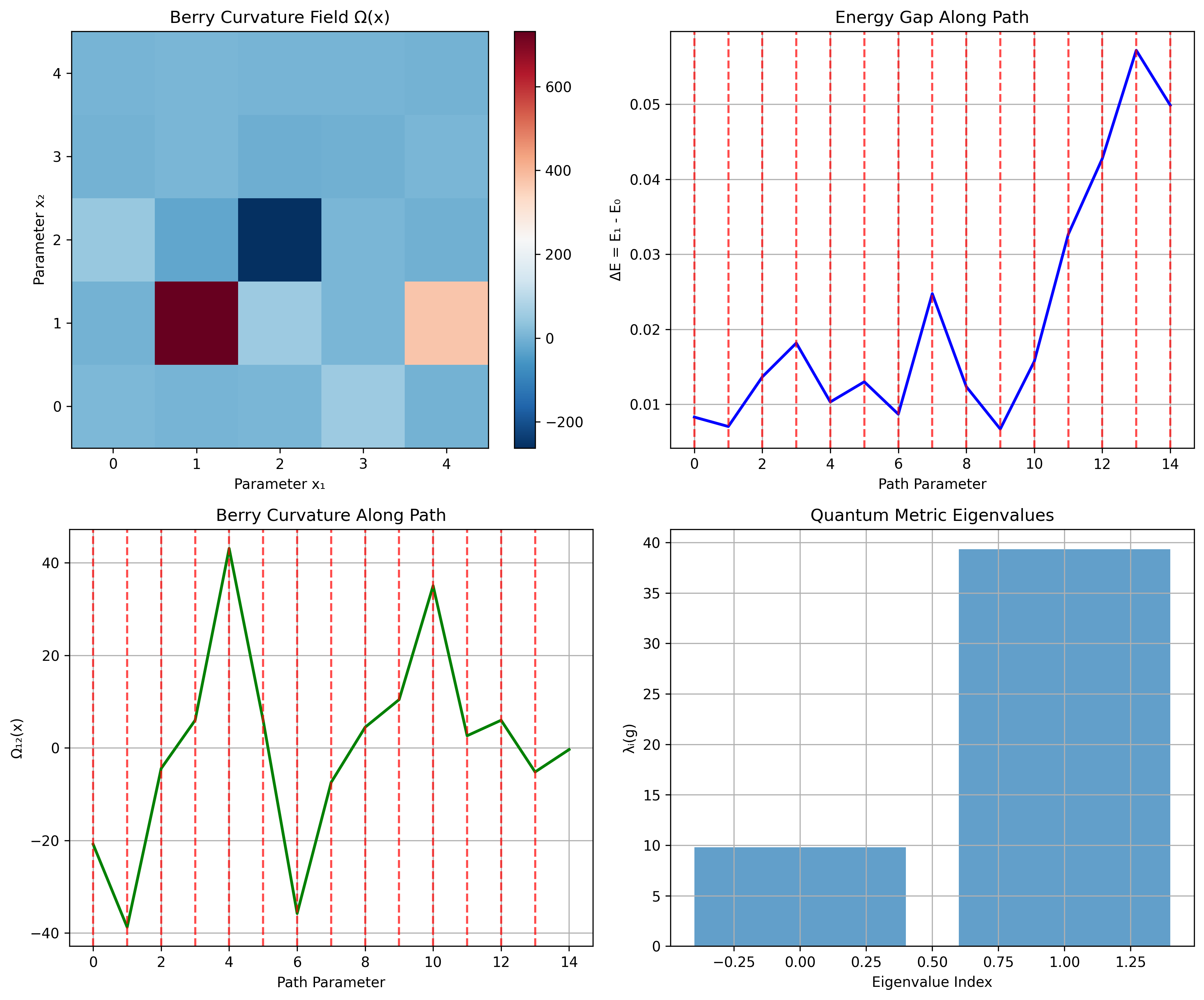
This visualization demonstrates the topological properties of the quantum system:

• Berry Curvature Field: Spatial distribution of topological curvature

• Chern Numbers: Topological invariants computed around closed paths

• Phase Transitions: Detection of quantum phase transitions in parameter space

• Topological Charge: Local topological properties

Analysis Results Summary

Key Results from Geometric Analysis Demo

Topological Analysis: - Berry curvature at sample point: 34.29 - Chern number around circle: 1.42 - Detected 28 phase transitions - Topological charge: 1.37

Quantum Information Measures: - Von Neumann entropy: 0.000002 - Entanglement entropy: 0.644 - L1 coherence: 4.58 - Relative entropy coherence: 2.20 - Information capacity: 0.000001 - Effective dimension: 1.000002

Berry Curvature Field: - Field computed on 8×8 grid - Mean curvature: 0.18 - Standard deviation: 3.16

Complete Analysis Pipeline: - Parameter dimension: 2 - Hilbert dimension: 8 - Sample Berry curvature: -20.86 - Quantum metric trace: 49.13

Technical Details

The visualizations were generated using:

• Framework: QGML (Quantum Geometric Machine Learning)

• Backend: PyTorch

• Hilbert Space Dimension: 8

• Parameter Space Dimension: 2

• Analysis Points: 12-20 points for comprehensive analysis

• Grid Resolution: 8×8 for Berry curvature field

The analysis demonstrates QGML’s capability to:

1. Encode classical data in quantum states using geometric principles

2. Compute topological invariants like Berry curvature and Chern numbers

3. Analyze quantum information through entropy and coherence measures

4. Detect phase transitions in parameter space

5. Visualize complex relationships between geometric and information-theoretic properties

Next Steps

These visualizations provide a foundation for:

• Real-world applications: Testing on biological, financial, or scientific datasets

• Scalability analysis: Extending to higher-dimensional parameter spaces

• Hardware implementation: Porting to quantum computing platforms

• Advanced correlations: Exploring deeper relationships between topology and information

For more detailed analysis results, see the JSON files in the test_outputs directory.